Special Points in a Triangle
Special Points in a Triangle: Overview
This topic covers concepts such as Special Points in Triangle, Centroid of a Triangle, Coordinates of Centroid in Triangle, Property of Centroid, Incentre of a Triangle, Coordinates of Incentre, Property of Incentre, Excentre of a Triangle, etc.
Important Questions on Special Points in a Triangle
Let be the median of the triangle with vertices and . The equation of the line passing through and parallel to is
Two vertices of a triangle are and If orthocentre of the triangle is the origin, find the coordinates of the third vertex.
A triangle has angles and . The orthocentre of the triangle will lie on the _____ of the triangle.
A triangle has angles and . The orthocentre of the triangle will lie _____ the triangle.
A triangle has angles and . The orthocentre of the triangle will lie _____ the triangle.
In medians and intersect at and . What is the area of ?
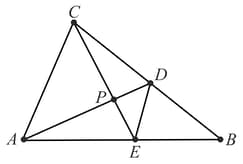
If and are such that , then the internal bisector of always passes through
Orthocentre of the triangle formed by the lines and is
If and are centroid, orthocenter and circumcenter of a triangle and then
The incentre of the triangle with vertices , and is
The orthocentre of the triangle with vertices and is
The orthocentre of the triangle with vertices and is
If and are three medians of the then .
Let and be the two medians of a and be their intersection. Also let cut at . Then is .
is the median of the triangle and is the centroid of . Then is .
If is the centroid of a and is any other point in the plane, then is equal to
The bisectors of angles and of a scalene triangle meet at What is the point called? Incentre Incircle Circumcircle.
Perpendicular bisectors of the sides and of a triangle meet at . What do you call the point ? Circumcenter Circumradius Circumcircle.
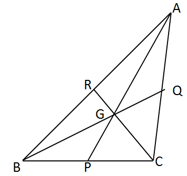
Point G is the centroid of .
If then ?
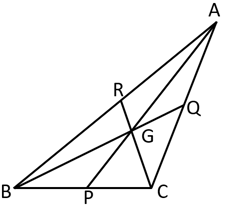
Point is the centroid of . If , then find .
